14.8: Lagrange Multipliers
- Page ID
- 936
Many applied max/min problems take the form of the last two examples: we want to find an extreme value of a function, like \(V=xyz\), subject to a constraint, like \( 1=\sqrt{x^2+y^2+z^2}\). Often this can be done, as we have, by explicitly combining the equations and then finding critical points. There is another approach that is often convenient, the method of Lagrange multipliers.
It is somewhat easier to understand two variable problems, so we begin with one as an example. Suppose the perimeter of a rectangle is to be 100 units. Find the rectangle with largest area. This is a fairly straightforward problem from single variable calculus. We write down the two equations: \(A=xy\), \(P=100=2x+2y\), solve the second of these for \(y\) (or \(x\)), substitute into the first, and end up with a one-variable maximization problem.
Let's now think of it differently: the equation \(A=xy\) defines a surface, and the equation \(100=2x+2y\) defines a curve (a line, in this case) in the \(x\)-\(y\) plane. If we graph both of these in the three-dimensional coordinate system, we can phrase the problem like this: what is the highest point on the surface above the line? The solution we already understand effectively produces the equation of the cross-section of the surface above the line and then treats it as a single variable problem. Instead, imagine that we draw the level curves (the contour lines) for the surface in the \(x\)-\(y\) plane, along with the line (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): Constraint line with contour plot of the surface \(xy\).
Imagine that the line represents a hiking trail and the contour lines are, as on a topographic map, the lines of constant altitude. How could you estimate, based on the graph, the high (or low) points on the path? As the path crosses contour lines, you know the path must be increasing or decreasing in elevation. At some point you will see the path just touch a contour line (tangent to it), and then begin to cross contours in the opposite order---that point of tangency must be a maximum or minimum point. If we can identify all such points, we can then check them to see which gives the maximum and which the minimum value. As usual, we also need to check boundary points; in this problem, we know that \(x\) and \(y\) are positive, so we are interested in just the portion of the line in the first quadrant, as shown. The endpoints of the path, the two points on the axes, are not points of tangency, but they are the two places that the function \(xy\) is a minimum in the first quadrant.
How can we actually make use of this? At the points of tangency that we seek, the constraint curve (in this case the line) and the level curve have the same slope---their tangent lines are parallel. This also means that the constraint curve is perpendicular to the gradient vector of the function; going a bit further, if we can express the constraint curve itself as a level curve, then we seek the points at which the two level curves have parallel gradients. The curve \(100=2x+2y\) can be thought of as a level curve of the function \(2x+2y\); Figure \(\PageIndex{2}\) shows both sets of level curves on a single graph. We are interested in those points where two level curves are tangent---but there are many such points, in fact an infinite number, as we've only shown a few of the level curves. All along the line \(y=x\) are points at which two level curves are tangent. While this might seem to be a show-stopper, it is not.
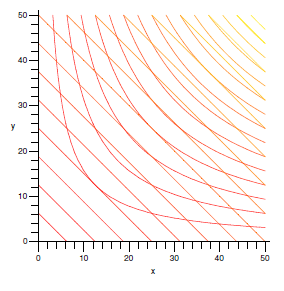
The gradient of \(2x+2y\) is \(\langle 2,2\rangle\), and the gradient of \(xy\) is \(\langle y,x\rangle\). They are parallel when \(\langle 2,2\rangle=\lambda\langle y,x\rangle\), that is, when \(2=\lambda y\) and \(2=\lambda x\). We have two equations in three unknowns, which typically results in many solutions (as we expected). A third equation will reduce the number of solutions; the third equation is the original constraint, \(100=2x+2y\). So we have the following system to solve:
\[2=\lambda y \qquad 2=\lambda x\qquad 100=2x+2y.\]
In the first two equations, \(\lambda\) can't be 0, so we may divide by it to get \(x=y=2/\lambda\). Substituting into the third equation we get
\[\eqalign{ 2{2\over \lambda}+2{2\over \lambda}&=100\cr {8\over100}&=\lambda\cr }\]
so
\[x=y=25.\]
Note that we are not really interested in the value of \(\lambda\)---it is a clever tool, the Lagrange multiplier, introduced to solve the problem. In many cases, as here, it is easier to find \(\lambda\) than to find everything else without using \(\lambda\).
The same method works for functions of three variables, except of course everything is one dimension higher: the function to be optimized is a function of three variables and the constraint represents a surface---for example, the function may represent temperature, and we may be interested in the maximum temperature on some surface, like a sphere. The points we seek are those at which the constraint surface is tangent to a level surface of the function. Once again, we consider the constraint surface to be a level surface of some function, and we look for points at which the two gradients are parallel, giving us three equations in four unknowns. The constraint provides a fourth equation.
Example \(\PageIndex{1}\)
Recall example 14.7.8: the diagonal of a box is 1, we seek to maximize the volume. The constraint is \( 1=\sqrt{x^2+y^2+z^2}\), which is the same as \(1=x^2+y^2+z^2\). The function to maximize is \(xyz\). The two gradient vectors are \(\langle 2x,2y,2z\rangle\) and \(\langle yz,xz,xy\rangle\), so the equations to be solved are
\[\eqalign{ yz&=2x\lambda\cr xz&=2y\lambda\cr xy&=2z\lambda\cr 1&=x^2+y^2+z^2\cr } \nonumber\]
If \(\lambda=0\) then at least two of \(x\), \(y\), \(z\) must be 0, giving a volume of 0, which will not be the maximum. If we multiply the first two equations by \(x\) and \(y\) respectively, we get
\[\eqalign{ xyz&=2x^2\lambda\cr xyz&=2y^2\lambda\cr }\nonumber\]
so \(2x^2\lambda=2y^2\lambda\) or \(x^2=y^2\); in the same way we can show \(x^2=z^2\). Hence the fourth equation becomes \(1=x^2+x^2+x^2\) or \(x=1/\sqrt3\), and so \(x=y=z=1/\sqrt3\) gives the maximum volume. This is of course the same answer we obtained previously.
Another possibility is that we have a function of three variables, and we want to find a maximum or minimum value not on a surface but on a curve; often the curve is the intersection of two surfaces, so that we really have two constraint equations, say \(g(x,y,z)=c_1\) and \(h(x,y,z)=c_2\). It turns out that at points on the intersection of the surfaces where \(f\) has a maximum or minimum value,
\[\nabla f=\lambda\nabla g+\mu \nabla h.\]
As before, this gives us three equations, one for each component of the vectors, but now in five unknowns, \(x\), \(y\), \(z\), \(\lambda\), and \(\mu\). Since there are two constraint functions, we have a total of five equations in five unknowns, and so can usually find the solutions we need.
Example \(\PageIndex{2}\)
The plane \(x+y-z=1\) intersects the cylinder \(x^2+y^2=1\) in an ellipse. Find the points on the ellipse closest to and farthest from the origin.
Solution
We want the extreme values of \(f=\sqrt{x^2+y^2+z^2}\) subject to the constraints \(g=x^2+y^2=1\) and \(h=x+y-z=1\). To simplify the algebra, we may use instead \(f=x^2+y^2+z^2\), since this has a maximum or minimum value at exactly the points at which \(\sqrt{x^2+y^2+z^2}\) does. The gradients are
\[\nabla f =\langle 2x,2y,2z\rangle\qquad \nabla g = \langle 2x,2y,0\rangle\qquad \nabla h = \langle 1,1,-1\rangle,\nonumber\]
so the equations we need to solve are
\[\eqalign{ 2x&=\lambda 2x+\mu\cr 2y&=\lambda 2y+\mu\cr 2z&=0-\mu\cr 1&=x^2+y^2\cr 1&=x+y-z.\cr }\nonumber\]
Subtracting the first two we get \(2y-2x=\lambda(2y-2x)\), so either \(\lambda=1\) or \(x=y\). If \(\lambda=1\) then \(\mu=0\), so \(z=0\) and the last two equations are
\[1=x^2+y^2\qquad\hbox{and}\qquad 1=x+y.\nonumber\]
Solving these gives \(x=1\), \(y=0\), or \(x=0\), \(y=1\), so the points of interest are \((1,0,0)\) and \((0,1,0)\), which are both distance 1 from the origin. If \(x=y\), the fourth equation is \(2x^2=1\), giving \(x=y=\pm1/\sqrt2\), and from the fifth equation we get \(z=-1\pm\sqrt2\). The distance from the origin to \((1/\sqrt2,1/\sqrt2,-1+\sqrt2)\) is \(\sqrt{4-2\sqrt2}\approx 1.08\) and the distance from the origin to \((-1/\sqrt2,-1/\sqrt2,-1-\sqrt2)\) is \(\sqrt{4+2\sqrt2}\approx 2.6\). Thus, the points \((1,0,0)\) and \((0,1,0)\) are closest to the origin and \((-1/\sqrt2,-1/\sqrt2,-1-\sqrt2)\) is farthest from the origin.
The Java applet shows the cylinder, the plane, the four points of interest, and the origin.
Contributors
Integrated by Justin Marshall.


